May 22nd, 2024
A Quick Look at the Chi-Square Test of Independence
By Rahul Sonwalkar · 7 min read

Overview
The Chi-Square Test of Independence is a vital statistical tool used to analyze the relationship between two categorical variables. This test is particularly useful in various fields, including social sciences, marketing, and healthcare, to understand associations and make informed decisions. This blog will explore the Chi-Square Test of Independence, its calculation, hypotheses, and how tools like Julius can assist in this statistical endeavor.
What is the Chi-Square Test of Independence?
The Chi-Square Test of Independence assesses whether there is a significant relationship between two nominal (categorical) variables. It compares the frequency of each category of one variable across the categories of another. The data is typically displayed in a contingency table, with rows representing categories of one variable and columns for the other.
Example: Gender and Empathy
Consider a researcher examining the relationship between gender (male vs. female) and empathy (high vs. low). The Chi-Square Test of Independence can determine if gender is associated with levels of empathy, such as whether more females than males are categorized as high in empathy.
Calculating the Chi-Square Statistic
1. Expected Values: First, calculate the expected values for each cell in the contingency table using the formula:

2. Chi-Square Statistic: Next, apply the formula:
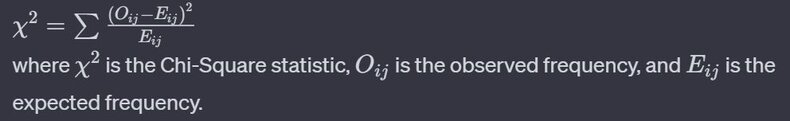
3. Degrees of Freedom: Calculate the degrees of freedom (DF) using:

Hypotheses in the Chi-Square Test
- Null Hypothesis: Assumes no association between the two variables.
- Alternative Hypothesis: Indicates an association between the variables.
- Alternative Hypothesis: Indicates an association between the variables.
Hypothesis Testing
The process involves computing the Chi-Square statistic and comparing it to a critical value determined by the significance level (usually 0.05) and the degrees of freedom. If the observed Chi-Square is greater than the critical value, the null hypothesis is rejected, indicating a significant association between the variables.
The Role of Julius in Chi-Square Test Analysis
Julius, an advanced statistical tool, can significantly streamline the Chi-Square Test of Independence:
- Automated Calculations: Julius can swiftly compute expected values, the Chi-Square statistic, and degrees of freedom, ensuring accuracy and efficiency.
- Data Organization: It assists in organizing data into a contingency table, simplifying the initial steps of the analysis.
- Hypothesis Testing: Julius provides an easy-to-understand interpretation of the test results, including whether to reject or accept the null hypothesis.
- Visualization: It offers visual representations, such as bar charts or heat maps, to illustrate the relationship between the categorical variables clearly.
Conclusion
The Chi-Square Test of Independence is an essential statistical tool for analyzing categorical data. Understanding how to perform this test and interpret its results is crucial for researchers and analysts across various disciplines. With the aid of tools like Julius, the process becomes more accessible, allowing for more accurate and reliable conclusions. By mastering the Chi-Square Test of Independence, you can uncover significant associations in your data, leading to deeper insights and more informed decision-making.
