July 24th, 2024
Guide to Inferential Statistics: Definition, Types, and More
By Josephine Santos · 7 min read
Imagine that you have a large population for which you want to make an estimate. A dataset full of college students, for example, where you want to figure out the mean grade across the entire set. Alternatively, you might have a hypothesis that you want to test – the relationship between those grades and factors like family income or living conditions.
How do you pull out the information you need from your sample data to draw conclusions?
Inferential statistical analysis is your answer – a method to analyze data so you can draw inferences about the population data within a sample. But what is it, exactly? And how can you use inferential statistics to examine an entire population?
What Are Inferential Statistics?
You have a large batch of population data. Your goal is to analyze that data – or samples obtained from it – to draw conclusions and make generalizations about the population. Inferential statistics is the branch of statistics that allows you to do that.
The technical definition is that this branch of statistics allows you to draw those conclusions by extracting random samples from your dataset. Using that random sample – usually called the “sample mean” – you make inferences about the entire population.
For instance, our college grades example from the introduction might see you take a random sample of 5,000 students’ results from hundreds of thousands across the country. Your analysis of those results allows you to make a generalization relating to the entire population.
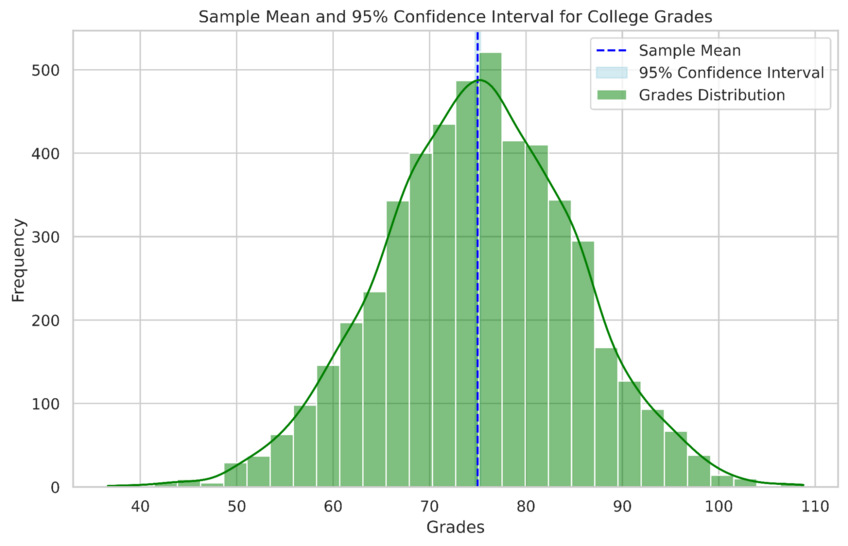
Inferential statistics example measuring the average grade for a college student based on an example data set of 5,000 students. Created in seconds with Julius AI
Why They’re Important
It all lies in explanation – inferential statistics allows you to draw conclusions based on extrapolation that can apply to a large population.
There’s also a practical component at play here. Returning to our college students example, around two million people graduate in the U.S. each year. That’s a huge dataset – one that’s almost impossible to analyze in totality. It’s here where inferential statistics shine. You can pull a random sample from that massive dataset that is more manageable while still allowing you to draw conclusions about the entire population.
Understanding the 2 Types of Inferential Statistics
There are two main types of inferential statistics – hypothesis testing and regression analysis – with each serving a different purpose within this branch of statistics.
Hypothesis Testing
Hypothesis testing is a straightforward concept – you have a belief or assumption about your population, and you need to check if that belief or assumption is correct. You’ll start by setting up your assumption (a “null hypothesis”) as well as setting up an alternative hypothesis that opposes the assumption you’ve made.
Then, you test. Through inferential statistics, you’ll draw the value of a test statistic, as well as confidence intervals and the dataset’s critical value. But this isn’t a one-test thing.
There are several types of hypothesis testing that fall under the inferential statistics banner:
- Z Test: Used for data with a sample size of at least 30 and a normal distribution. You’ll find the means of your sample – as well as the full population – to see if they’re equal assuming you know the population variance.
- F Test: Take two samples and an F Test will tell you if there’s a difference in the variance between those samples.
- T Test: If you don’t know the population variance and have a sample size of less than 30, you’ll use a T Test instead of a Z test.
As for the previously mentioned confidence intervals, these are measures of your confidence that a test conducted on multiple samples under the same conditions will produce an expected result. The higher the confidence interval – such as 95% - the more likely you are to get the results you expected.
Regression Analysis
Though there are many types of regressions – including nominal and ordinal – you’ll usually use inferential statistics to calculate linear regression. This is a measure of the impact that an independent variable has on a dependent variable.
Inferential vs. Descriptive Statistics
Conclusions or quantification?
That’s the main question to ask when choosing between the inferential and descriptive statistics models. Though both are used to make generalizations about a dataset – and often to describe the data within it – there are key differences to keep in mind.
Inferential
Inferential statistics is all about conclusions – you create hypotheses and use analytical tools on your sample data to determine a conclusion. You’ll make inferences about populations for which you might not know everything based on samples that deliver key information.
Descriptive
With description statistics, you’re not looking to infer anything from the data. You’re just quantifying what you have and determining the dataset’s general characteristics. You’ll usually have a known sample, allowing you to work out means, medians, ranges, and variances within that sample.
Examples of Inferential Statistics
We’ve touched on one example already – examining college students’ grades. If you have a sample of 5,000 grades that you know to be correct, you can use that sample to determine the mean marks for every college student in the country. It’s an approximate figure, with a larger population leading to a more accurate conclusion.
Take that example and you can see how inferential statistics apply to any dataset that has a large population. Median income in the United States, for instance, can be worked out not by looking at around 250 million income figures, but by pulling a random sample from that huge population for analysis.
How to Utilize Inferential Statistics
Almost all ventures into inferential statistics start with a question. From that question, you create a null hypothesis – along with an alternative – that defines the answer you believe to be true for that question.
Then, you collect sample data and choose the appropriate test to perform – regression, hypothesis, or both. That test delivers results, through which you create a conclusion to determine either the relationships between the variables in your test (regression testing) or the validity of your assumptions (hypothesis testing).
Make the Most of Statistical Analysis with Julius AI
Setting population parameters. Collecting data points. It can all start to feel like a little too much for you to do manually, especially when you’re working with a large population. There’s so much data to sift through – and so many opportunities for things to go wrong – that you may not feel confident enough to accept or reject the null hypothesis you’ve formed even if you think you’ve done everything correctly.
So, lighten your load. With Julius AI, you get a computational AI tool that takes seconds to analyze data that might take you hours – or even days – to analyze. Better yet, the tool draws insights, visualizes your data, and provides accurate conclusions based on the data sources you feed into it.
Sign up for Julius AI today – it’s your ticket to faster and more accurate inferential statistical analysis.
Frequently Asked Questions (FAQs)
What are the five elements of an inferential statistical analysis?
The five key elements of inferential statistical analysis are population, sample, hypothesis, statistical test, and inference. You start by identifying the population and selecting a representative sample, then formulate a hypothesis and choose an appropriate statistical test to analyze the data. Finally, the results are interpreted to make generalizations or draw conclusions about the entire population.
What are the common statistical tools used in inferential statistics?
Common statistical tools for inferential statistics include hypothesis tests (e.g., Z tests, T tests, and F tests), regression analysis, confidence intervals, and ANOVA (Analysis of Variance). These tools help identify relationships, test assumptions, and make predictions or generalizations based on sample data.
