March 8th, 2024
What Is Statistical Power Analysis & Why Does It Matter?
By Connor Martin · 6 min read
Statistical power analysis helps researchers design the most effective, worthwhile studies and experiments. It minimizes the risk of error and is an invaluable process for research optimization. But for those without much experience, it’s quite a complicated concept.
This guide breaks down what statistical power analysis is and why it’s so valuable.
What Is Statistical Power?
Statistical power, or sensitivity as it’s sometimes known, is a measurement of how likely a study is to detect an effect. In simpler terms, it’s a sign of how effective a study is.
As an example, imagine you’re studying a new form of fertilizer. You believe it helps plants produce more crops, and you want to prove that. By working out the statistical power of your study, you can see how likely it is to confirm your hypothesis.
- A high-power study is likely to detect the desired effect and confirm the hypothesis.
- A low-power study is less likely to confirm the hypothesis and more likely to encounter errors.
Power is influenced by a range of key factors, including sample size and significance level (more on those below).
What Is Power Analysis?
Power analysis is the process of calculating the statistical power of a study and determining what size sample you need to detect an effect and prove your hypothesis.
Naturally, the best time to conduct a statistical power analysis is when designing a study, before you start to collect any data because it helps you figure out how much data you need to gather.
Let’s return to our previous example to see how this works.
If you want to test the effects of fertilizer on crop yields, you could devise a simple experiment. You might plant crops in two different fields, and only apply the fertilizer in one of them. Then, you can wait for harvest time, measure the yields of each field, and compare them. Ideally, you’re hoping to find that the plants in the fertilized field produce more crops.
A statistical power analysis will help you work out the optimal number of plants to use to successfully detect an effect. In other words, it’ll help you set up your experiment to be successful.
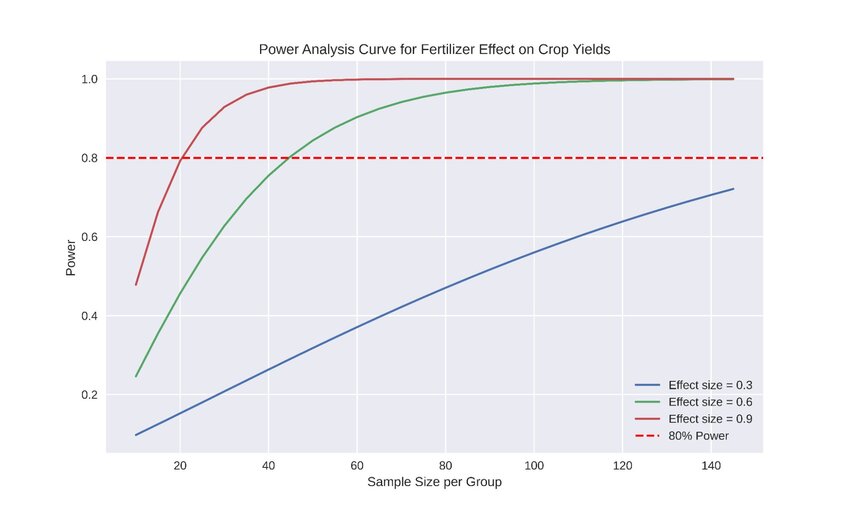
Example power analysis that shows the relationship between sample size and power for different effect sizes. Created in seconds with Julius AI
Factors That Affect Power
As mentioned above, a range of factors can affect statistical power. Here’s a glimpse at the most popular ones.
Sample Size
Sample size has a direct correlation to statistical power. If you use a bigger sample, the power of your study increases, as you’ll gather more data and thereby conduct a more accurate, reliable test.
Significance Level
The significance level of any test or study is the chance of encountering a Type I error. A Type I error is when you reach a conclusion that isn’t actually accurate. Typically, it’s set at 5%.
Effect Size
The effect size of a study is just what it sounds like – the size or magnitude of the effect you’re trying to detect. In our previous example, the effect size would be the amount of yield increase in the crops, which could be small and hard to detect or quite large if the fertilizer is particularly powerful.
Variability
Variability refers to the presence of variance in your sample population. More variability means lower power, as there are more variables in play that could impact the test results and make it harder to prove your specific hypothesis.
Measurement Error
Measurement error refers to the implied level of error in taking measurements, or the difference between an entity’s true value and its measured value. There’s always a certain margin of error when measuring things, and this has to be taken into account - higher measurement error means lower power.
Why Is Power Analysis Important in Statistics?
Statistical power analysis is important because of the value it brings to a study, and how much it can help you reach an accurate and evidence-based conclusion.
When you’re testing any hypothesis, you always have both a null or no effect hypothesis and a hypothesis of true effect, which is the idea you’re trying to prove. Your goal is to gather as much data as is necessary to reject the null hypothesis and demonstrate the hypothesis of true effect.
However, you also have to manage the risks of Type I and Type II errors while conducting your study. We’ve already covered Type I errors, but a Type II error is when your alternative hypothesis is actually true, but you don’t gather enough data to see it.
By working out and optimizing the statistical power of your study, via statistical power analysis, you can reduce your risk of errors and maximize your potential for success.
How Can You Increase Power?
Ideally, you’ll want quite a high level of statistical power (around 80% is the usual standard) before beginning any study. Here are some ways to increase it:
- A bigger sample size. More samples tested means more data collected and therefore more power.
- A larger effect sample size. If your effect is easier to detect, the statistical power of your study should increase.
- Higher level of significance. This will effectively make your test more sensitive, and thereby increase its power.
- Measure more accurately. By reducing your margins of measurement error, you'll also minimize variability in your study and make it more effective and reliable.
Other Tips for Power Analysis
A statistical power analysis is only effective if carried out effectively and accurately. You have to be as precise as possible when working out the relevant factors that influence statistical power. The best way to do this is by using the most trusted, accurate technological solutions, like AI. AI data analyst tools can conduct detailed statistical power analysis on your behalf.
Make Statistical Analysis Easy and Quick with Julius AI
Statistical power analysis is an invaluable part of statistics and study design, helping researchers save time and resources, while also optimizing their study plans. However, it can be quite tricky to carry out an accurate statistical power analysis and make the most of this technique.
Julius AI can help with that. As a leading AI data analyst, Julius AI can carry out statistical power analysis for you. Just enter a quick prompt and some basic data about your study, and let Julius AI do the rest. It’s the fastest, easiest way to do power analysis.
Frequently Asked Questions (FAQs)
What does 80% statistical power mean?
An 80% statistical power means that your study has an 80% chance of detecting an effect if it truly exists. This level of power is often considered the gold standard, as it balances the likelihood of avoiding Type II errors (failing to detect an effect) with practical constraints like sample size.
How do you discuss statistical power?
When discussing statistical power, highlight its importance in reducing the risk of errors and ensuring reliable results. Include details about the power level chosen (e.g., 80%), the factors influencing it (like sample size and effect size), and its role in confirming or rejecting hypotheses in your study.
What is good statistical power?
Good statistical power is typically considered to be 80% or higher. This level ensures a strong likelihood of detecting an effect if it exists while maintaining an acceptable balance between Type I and Type II error rates.
What is the minimum sample size for statistical significance?
The minimum sample size for statistical significance varies depending on factors like effect size, significance level (commonly 0.05), and desired power (commonly 80%). A power analysis can help determine the exact sample size needed for your specific study. For smaller effects, larger sample sizes are usually required.
